今回のテーマは「分数の基本」です!
分数は小学校で習いますが、
通分や約分といった、分数特有の計算が苦手な生徒も多いので、つい計算ばかりに気がいってしまいます。
もちろん、分数の計算ができることはとても重要ですが、
同時にその考え方や使い方、つまり「分数のキモチ」を理解することも大切です!
そこで今回は、分数の基本的な考え方にスポットを当ててお話ししていこうと思います。
それでは、今回の項目です。
step
1分数は「割合」や「比」を表す道具
step
2「割合」と「比」を別々に考えない
step
3「確率も分数」
※以下「5分の1」などは「1/5」で表します。
分数は「割合」や「比」を表す道具
冒頭でも言ったように、分数は計算が全てではありません。
「2/5」という分数を考えてみましょう。
これは「5個に分けたうちの2つ分」という「割合」を表します。
例えば、1000円の「2/5」はいくらか、を考えるときを考えてください。
1000円の「2/5」
一般的な解説などでは「1000」×「2/5」と計算しますが、
割り算を入れて考えると、「1000÷5×2」で求めます。
最初の「1000÷5」は、「1000を5等分したときの1つ分」です。
(※割り算は均等に分ける計算です。)
これは1000×1/5と同じです。
そして「その2つ分」を考えるので、「×2」
つまり、
1000÷5×2
=1000×1/5×2
=1000×2/5
となります。
どうでしょうか。
これで1000円の「2/5」は、
1000円を「5個に分けたうちの2つ分」と言い換えることができる、
ということが理解できたのではないでしょうか。
割り算の公式で、「比べる量」を求めるときには、
「もとにする量」×「割合」=「比べる量」となるのはこのためです!
さらに、「比」は分数とも関係しています!
具体例で考えてみましょう。
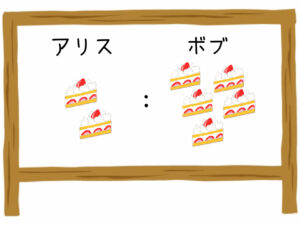
アリスとボブが、ケーキを「2:5」の比で分けたとしましょう。
このとき、「2/5」という分数はどんな意味を表すでしょうか?
さっきの割合の考え方を使うと、「5個に分けたうちの2つ分」ですから、
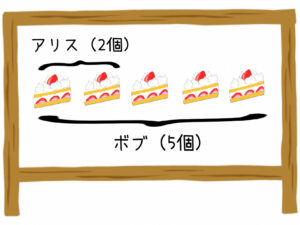
「ボブのケーキを5としたとき、アリスのケーキはそのうち(ボブでの5等分の1つ)の2つ分」
ということになります!
形は分数になっても、比の意味は変わってないですよね!
つまり「分数」を用いることで、「比」を「割合」として見ることができるのです!
さらに上の図を見てください。
このようにすると線分図で比を確認する理由もわかるのではないでしょうか。
どうですか?
分数が、算数のいろんな場面で用いられていますよね。
このように、「分数」は「割合」や「比」を表すための一つの道具です。
だからこそ、「分数のキモチ」を理解することがとても重要なんです!
ココがポイント
分数は「等しく分ける事」、これが「分数のキモチ」。
「割合」と「比」を別々で考えない
さて、1000円とケーキの例でもお話ししたように、
分数を用いることで「割合」と「比」の関係が見えてきました。
形が違うだけで、中身はほとんど同じでしたよね!
しかしよく、「割合」と「比」を完全に別物と捉えている生徒がいます。
こういう子は、
図形の問題で、線分比が分数で表されていることに違和感を感じていたり、
割合と比がミックスされた問題でつまずいたりします。
これは割合と比の単元で扱う用語が変わってくることが考えられます。
分数を
割合の単元では「割合」と言い、
比の単元では「比の値」と呼びます。
(食塩水の問題では%表記を用いますが「濃度」とも言われますね。)
そこで分数をこのように考えてはいかがでしょうか。
分数の捉え方
分母は「分ける数の個数(全体)」と捉え、
分子は「そのうちの一部分」
いかがでしょうか。
先ほどの例の割合と比の内容に共通していませんか。
言い方はお子様がわかりやすい言葉に置き換えてもらえればいいと思います。
とにかく、
分母=分ける個数(もしくは全体の個数)
分子=そのうちの一部
が理解できたうえで、
割合や比の問題をこのように見て考えることができれば、
単元は異なっても分数を駆使して解くことができるようになるかもしれません。
分数の例だけでなく、
こうした基本学習のつながりが理解できていないことで起きる間違いもあるので、
他分野との関係を知ることも大切です。
今回の場合は、分数を見たときに「割合」と「比」の両方で考えられるようになるということですね!
ココがポイント
分母=分ける個数(全体を分けた個数)、分子=そのうちの一部
「確率も分数」
さて分数は「割合」や「比」を表すものでした。では他には?
「確率」です!
確率は小学生では習わないので、先の例ではあえて外しましたが、
確率はどうなのでしょうか。
例えば、「2/5」という分数は、
確率の世界で「5回中2回起こる」という頻度を表します。
また、確率って百分率で表される事もありますよね。30%とか、80%とか。
そうです、確率は「割合」でもあるのです!
(※ただし確率の場合は100%を超えることはありません。)
「確率」→「分数で表される」→「割合」
これまで述べてきた分数の基本性質が理解できていれば、
確率を学習する際、
分数の形が出てきただけで「なるほどな!」と理解が速くなるはずです。
ここにも、他単元での基本学習のつながりが生きてくるのです。
ココがポイント
分数の基本的な考え方を使えば、より幅広い応用力を身に着けることができる。
まとめ
いかがでしたか?
今回は、分数の基本をテーマに、その考え方、使い方についてご紹介しました。
ここで取り上げた「割合」、「比」、「確率」は中学、高校でも必須の単元ですから、
これからの勉強に必ずつながります。
分数を教えるときは、ぜひ参考にしてみてください!
ポイントまとめ
- 分数は「等しく分ける事」、これが「分数のキモチ」
- 分母=分ける個数(全体を分けた個数)、分子=そのうちの一部
- 分数の基本的な考え方を使えば、より幅広い応用力を身に着けることができる
次に読むべき記事
国語の問題も心配だなぁというとき → 「国語の読解・記述を教える際に気を付けるべきポイント」【国語 記述問題の教え方-初心者編①】
意外と知られていない「記述問題が解けない」理由がわかる。
https://kategakublog.com/lc17-japanese-writing-beginner-01-overview/
点数が伸びない根本をしりたいとき → 「点数が伸びない原因(定期テスト)」:「努力の量」より「努力が点になる仕組み」
つまづきを「見える化」することで何をすればよいかが見えてくる。
https://kategakublog.com/c15-scores-not-improving-causes-2/
その他算数・数学の記事はこちら▼
小学1年生の繰り下がりの引き算
今回は、小学1年生の「繰り下がりの引き算」についての学習注意ポイントについてお話しします。 私が運営している学習塾でもここが解けなくて悔しい! と言って小学1年生の女の子が入塾してきたことがありました。 そんなに難しいことないでしょ? なんとなくで慣でやれるでしょ!? おっしゃる通りでございますが、 この単元、非常に重要な単元で、 教える側としても学ぶべきところがたくさんある単元です。 読み物としても興味深いと思うので是非最後までお読みいただければと思います。 基 ...
分数がわかれば割合もわかる!【割合・比・確率の共通点】
今回のテーマは「分数の基本」です! 分数は小学校で習いますが、 通分や約分といった、分数特有の計算が苦手な生徒も多いので、つい計算ばかりに気がいってしまいます。 もちろん、分数の計算ができることはとても重要ですが、 同時にその考え方や使い方、つまり「分数のキモチ」を理解することも大切です! そこで今回は、分数の基本的な考え方にスポットを当ててお話ししていこうと思います。 それでは、今回の項目です。 ※以下「5分の1」などは「1/5」で表します。 分数は「割合」や「比」を表す道具 冒頭でも言ったように、分数 ...
数学100点への道【まとめ】
学校の定期テストの数学で100点を取ることはとても難しいことです。 普段50点に達しないお子様にとっていきなり100点を取ることは無理です。 しかし、しっかりステップアップすることで決して無理な事ではありません。 これまでに50点に達しない生徒が100点を取ったその共通の方法をできるだけ完結にまとめて紹介します。 事前にはっきり言います。 「いきなり100点は無理です。」 時間はかかります。 中学校では無理でも高校で達成した生徒もいます。 ご家庭での応援も必要です。 その上でご参考にしていただければ幸いで ...
九九は暗記の後が重要!(覚えられない、かけ算で使えないを解消!)
今回は算数で誰もが通る「九九」についてです。 小学校の時に何度も暗唱して覚えましたよねー。 懐かしい思い出です! さてそんな九九ですが、 暗記の際にいくつか注意点があるので、 それについてお話ししていきます! では一つ一つ見ていきましょう! 1.そもそも九九って覚えないといけないの そもそも九九って暗記する必要あるの?って事ですが、 しなくても算数や数学を学ぶことは出来ます。 しかし、計算をする上では素早く行う上では必須となります。 また、学校のテストではできている上で問題数が設定されているので、学校でも ...
これで数学100点!満点にはケアレスミスが大敵【数学100点への道➂】
さて今回は【数学100点への道】完結編です。 ついに100点を目指すときがやってきました。 この記事は、現在数学90点前後を取っているお子様向けの内容になっています。 まだ全然そこまでいってません!という方は以下を先にご覧ください。 ⇒数学100点への道① ⇒数学100点への道② さて今回はいよいよ100点ですね! 基本や発展問題などへの取り組みはできているものとしてお話してきますね。 今回もポイントをできるだけ少なく簡潔になるようにまとめました。 今回のポイントはこちらです。 ではひとつひとつ見ていきま ...